Isopycnic diffusion:
Click here to get the tar
file for source codes (750 KBytes).
Click here to get the tar
file for Gmetas (18 MBytes).
Scientific interests
Nonlinear processes in geophysical fluid dynamics;
Vortex dynamics ;
Advanced numerical methods for convectively dominated flows;
Numerical treatment of contact discontinuities;
Computer simulation of
turbulent flows;
Multigrid methods and their applications in fluid mechanics;
Regional and basin scale ocean modeling;
Supercomputing and parallel processing;
Ongoing project: Regional Ocean
Modeling System
This is a collaborative effort with
Hernan Arango
and Dale Haidvogel
from ocean modeling
group of Institute of Marine and
Coastal Sciences, Rutgers university.
Re-engineering SCRUM
The goal here is to develop a new model which is capable to provide
reliable and more realistic high-resolution simulations for coastal and
basin scale configurations and which runs on the newest available
family of SGI/CRAY Origin 2000 supercomputers.
A descendant/successor of
SPEM and then
SCRUM family
topography following S-coordinate ocean models, the new model,
called regional Ocean Modeling System (ROMS)
drastically expands the capabilities of the existent
SCRUM-3.0 code in terms of numerical/computational performance,
grid resolution, as well as update of numerical techniques and
parameterizations of unresolved physical processes.
At first, the SCRUM-3.0 code was redesigned in order to comply with
the logically shared/physically distributed memory architecture of
the Origin 2000 and its synchronization strategy based the write-back
memory bus protocol and the global cache coherency mechanism.
The new model employs the explicit coarse-grained MP parallelization
paradigm, with subdomain partitioning (blocking) in both horizontal
dimensions.
The explicit MP model is a shared approach, which implies that the
parallel threads are created only once and exist during the whole
run time of the program.
Each parallel thread is self-aware in sense that it determines by itself
which subdomain(s) [tile(s)] it needs to process (rather than, say, waits
until the master thread will tell it what to do) and it is also aware
of the presence of the other threads.
Unlike classical message passing codes, the number of the subdomains
is not necessarily equal to the number of CPUs used, but rather chosen
in such a way that the storage segment associated with a subdomain
fits into the processor cache. Thus, if one needs to run a larger problem
on a given number of CPUs, it often turns out that it is more advantageous
to increase the number of subdomains, while approximately maintaining
their size, rather than keep the number of subdomains, while letting
their size to increase.
Explicit calls to barrier and lock functions are used to occasionally
synchronize the parallel threads.
Distribution of the model arrays across the multiple nodes of Cray Origin
is done relying on the "first touch" default distribution policy and the
affinity between memory placement and workload partitioning is kept
consistent throughout the whole duration of the model run.
Going beyond: from parallel version of SCRUM to ROMS
Unlike ocean model parallelization projects of the past, transition
from SCRUM to ROMS is not just a rewrite of the code for the purpose
of gaining computational speed. Once grid resolution is increased,
and the amount of dissipation in the model is decreased accordingly,
the flow regime is changing: it becomes turbulent and processes of
exchange due to vortex interactions become explicitly resolved.
In this situation the typical low second order accuracy finite difference
numerical schemes (which were used in ocean modeling for last 30 years)
are no longer the methods of choice. Higher-order accuracy (typically third-
and fourth-order) schemes, which are better tolerant to the non-smoothness
of the fields on the grid scale, are used instead.
It is interesting to note that, this choice is also encouraged by the
evolution of the computer architectures, due to fact that the processing
power of the machines tends to increase faster than the memory bandwidth.
Consequently, more sophisticated methods, which result into more
computationally dense programs utilize the resources of the machine in a
more balanced way, while the more traditional second-order accurate
methods, which were optimal for the computers of the past turned out to be
memory bound on the modern machines.
Future Plans
Building embedded coarse-fine grid coupling capability;
Data Assimilation capability;
Biological/ecosystem model
driven/coupled with the existent physical model;
Related links:
Patrick Marchesiello
(also here ),
Xavier Capet
( also here),
Francois Colas,
Emanuele Di Lorenzo,
Florian Lemarie ,
Art Miller ,
Bruce Cornuelle, John Moisan


Atlantic DAMEE project
Thought, ROMS was designed mostly for high-resolution coastal
configurations, Atlantic basin-scale simulations have became its
first proving ground.
Here are some results from our Atlantic "region" runs (yeah, we do
have ambition to build a model for the global region!).
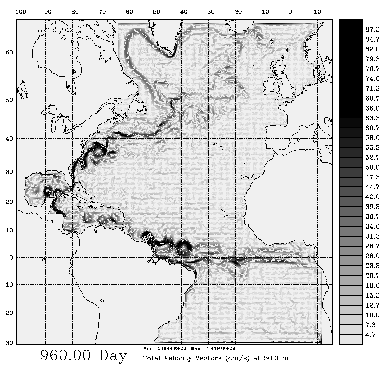
Fig. 1 Velocity at surface. Note that despite a relatively coarse
resolution of 3/8 degree, we have obtained a reasonably good pattern of
the Gulf Stream separation, which detaches off Cape Haterras and meanders.
This particular simulation was without any explicit viscosity or diffusivity
in horizontal direction, relying only on the hyperdiffusive truncation
error of a third-order accurate [in space and time] upstream biased advection
schemes, applied for both horizontal momentum and the tracer [temperature and
salinity] equations.
Click on image to display it in double size
Also note the remarkable nonlinear activity in the equatorial region.
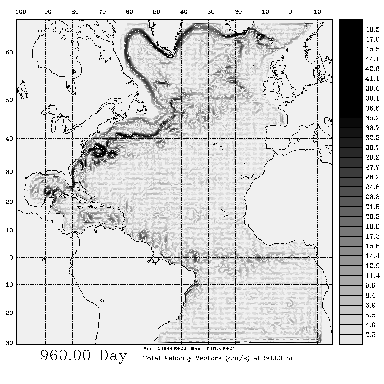
Fig. 2 Velocity at depth of 500 meters.
In comparison with Fig. 1,
one can no longer see the intense equatorial currents: these are too shallow,
and generally limited to the upper 200 meters. One can still see, however,
weak traces of the Equatorial undercurrent going to the west.
In contrast to that, deep current along Labrador coast is visually
intensified. It mets Gulf Stream and literally pushes it away from the coast.
Click on image to display it in double size
Also note that the anticyclonic surface circulation in the Gulf of Mexico
is no longer seen here; instead the deep cyclonic circulation is more
pronounced here.
Note that, compared to Fig. 1, velocity scale has been changed approximately
in three times, so that even if some vectors look darker than on Fig. 1, they
are not necessarily larger.
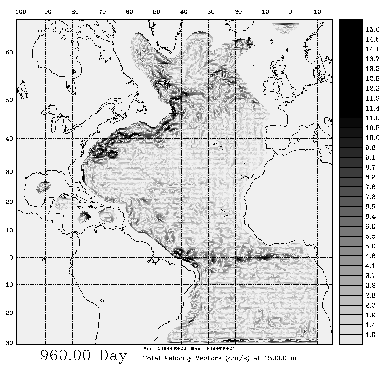
Fig. 3 Velocity at depth of 1500 meters. One can no longer see Gulf
Stream. Instead note the North Atlantic Countercurrent, heading all the way
from the Labrador Peninsula to Brazilian coast, crossing the equator.
Click on image to display it in double size
We believe that to a large degree this current topographically controlled.
Scrum, as a topography following S-coordinate model has no problem to simulate
this current correctly, even at such, relatively coarse resolution.
Also note the presence of topographically trapped circulations, especially
in deep regions of Gulf of Mexico and Carribean. These are generally cyclonic.
It is possible, that these are explained as topographically rectified flows
obtained from varying forcing. We cannot explain everything we see, however.
Velocity scale has been reduced again. Deep currents are generally
much less intense.
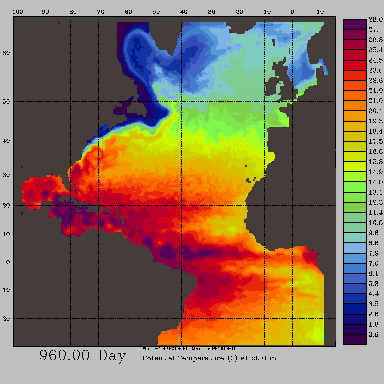
Fig. 4 Temperature at 50 meters. SUMMER.
Click on image to display it in double size
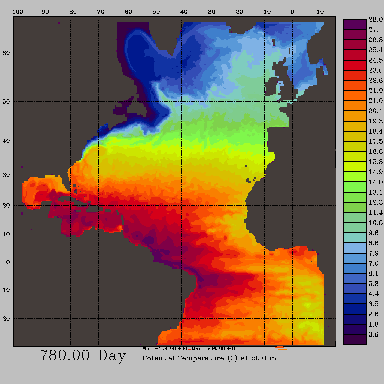
Fig. 5 Temperature at 50 meters. WINTER.
Click on image to display it in double size
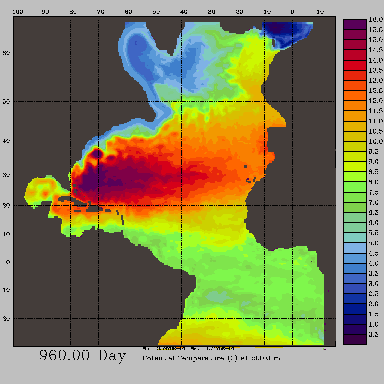
Fig. 6 Temperature at 500 meters. The same time as on Fig. 5 above.
Click on image to display it in double size
This computation was performed in the
National Centre for Supercomputing Applications (NCSA)
in Urbana-Champaign, Illinois.
Links related to this project :
Data Assimilation and Model Evaluation Experiments
US West Coast Modeling Project
US West Coast simulation is the main target for which ROMS is
designed. The key guy here is Patrick
Marchesiello, who happened to be the first user of the ROMS
since it was created. But since then he became one of the
developers. Here I am working mostly on mathematical and
computational aspects, while Patrick works on the physical formulation of
the problem and the model configuration (although in many cases the border
the border between these two groups is not well defined).
That is why all these pictures ended up here.
Here are few snapshots of sea surface temperature (SST)
illustrating seasonal cycle.
Model configuration is: curvilinear with grid resolution approximately 10 km
in both directions, approximately isotropic;
dimensions of the grid are 96 x 256 x 30 points, which results in approximately
250 MBytes of storage;
the model is forced by COADS monthly climatological winds as well as surface
heat and effective salt fluxes (fresh water evaporation/precipitation);
no explicit viscosity and diffusion (except in sponge layers
near the radiation open boundaries):
for this purpose we rely exclusively on the build-in hyperdiffusive
dissipation inherent for the third-order upstream biased advection schemes
used for both the momentum and the tracer equations.
It was run starting from the Middle of the May Levitus climatology fields
for temperature and salinity and zero initial velocities, hence it goes
through geostrophic adjustment after startup. It was spun up for two years,
and starting from the third year the result were analyzed. Day on the plots
below means Julian day.

Middle of May
This is just the beginning of the upwelling season. Note the band of cold water
near the coast.

Middle of July
This is the middle of summer. The overall temperature is increased due to
heat flux on surface, but the narrow band nearshore remains cold due to
upwelling.

Middle of September

Middle of November
Note that the upwelling near the coast is not so pronounced any more.
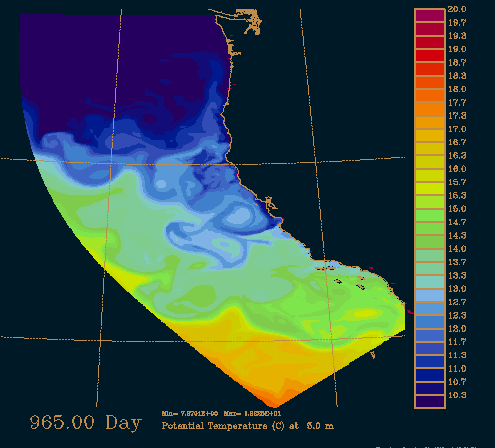
Middle of January
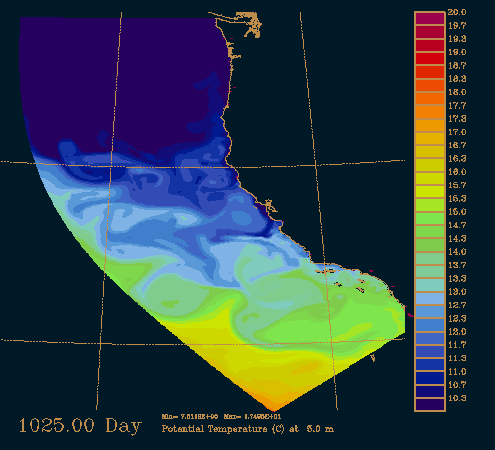
Middle of March
History
July 2008 to present time: Project Scientist,
Center for Earth
System Research (CESR),
Institute of Geophysics
and Planetary Physics (I.G.P.P.),
University of California at Los Angeles (UCLA).
Oct 1998 - June 2008:
Specialist. Geophysical Modeling. CESR, I.G.P.P., UCLA.
Primary developer of ROMS code.
May 1995 - Sept 1998: Programmer Analyst; I.G.P.P., UCLA.
Jan 1994 - Apr 1995 -- Post Doctoral Research Associate in
Center for
Ocean-Atmospheric Prediction Studies (COAPS),
Florida State University.
Aug 1992 - Nov 1993: Postdoc in the
Department of
Oceanography, Florida State University.
Education
1992 Ph.D. in Mechanics of Fluid, Gas and Plasma from
Moscow Institute of Physics and Technology
(MPTI),
Dolgoprudny, Moscow region, Rossia.
1988 Degree of engineer-physicist from MPTI.
Peer-reviewed Articles:
Shchepetkin, A. F., 2015: An adaptive, Courant-number-dependent implicit
scheme for vertical advection in oceanic modeling.
Ocean Modeling, accepted, in press,
doi:10.1016/j.ocemod.2015.03.006
PDF preprint
Lemaré, F., L. Debreu, A. F. Shchepetkin, and J. C. McWilliams, 2012:
On the stability and accuracy of the harmonic and biharmonic isoneutral
mixing operators in ocean models.
Ocean Modeling, 52-53 pp. 9-35,
doi:10.1016/j.ocemod.2012.04.007
Lemarié, F., J. Kurian, A. F. Shchepetkin, M. J. Molemaker, F. Colas,
and J. C. McWilliams, 2012: Are there inescapable issues prohibiting the
use of terrain-following coordinates in climate models?
Ocean Modeling, 42, pp. 57-79,
doi:10.1016/j.ocemod.2011.11.007
Mason, E., F. Colas, J. Molemaker, A. F. Shchepetkin, C. Troupin,
J. C. McWilliams, and P. Sangrà (2011), Seasonal variability of
the Canary Current: a numerical study,
J. Geophys. Res., Oceans, 116 , C06001,
doi:10.1029/2010JC006665
Shchepetkin, A. F. and J. C. McWilliams, 2011: Accurate Boussinesq oceanic
modeling with a practical, ``stiffened'' equation of state.
Ocean Modeling, 38, pp. 41-70,
doi:10.1016/j.ocemod.2011.01.010 ,
PDF preprint
Mason, E., J. Molemaker, A. F. Shchepetkin, F. Colas, J. C. McWilliams,
and P. Sangrà, 2010: Improved procedures for offline grid nesting
in regional ocean models. Ocean Modeling, 35, pp. 1-15,
doi:10.1016/j.ocemod.2010.05.007
Uchiyama, Y., J. C. McWilliams, and A. F. Shchepetkin, 2010: Wave-current
interaction in an oceanic circulation model with a vortex-force formalism:
Application to the surf zone. Ocean Modelling, 34, (1-2),
pp. 16-35,
doi:10.1016/j.ocemod.2010.04.002
Shchepetkin, A. F. and J. C. McWilliams, 2009: Correction and Commentary for
"Ocean Forecasting in Terrain-Following Coordinates: Formulation and Skill
Assessment of the Regional Ocean Modeling System" by Haidvogel et al.,
J. Comp. Phys. 227, pp. 3595-3624. J. Comput. Phys., 228,
pp. 8985-9000,
doi:10.1016/j.jcp.2009.09.002 ,
PDF preprint
McWilliams, J. C., E. Huckle, and A. F. Shchepetkin, 2009: Buoyancy effects
in a stratified Ekman Layer J. Phys. Oceanogr., 39,
pp. 2581-2599.
doi:10.1175/2009JPO4130.1
Colas, F., X. Capet, J. C. McWilliams, and A. Shchepetkin, 2008: 1997-1998
El Nino off Peru: A numerical study.
Progress in Oceanogr., 79, No 2-4, pp. 138-155,
doi:10.1016/j.pocean.2008.10.015
Shchepetkin, A. F. and J. C. McWilliams, 2008: Computational kernel
algorithms for fine-scale, multi-process, long-term oceanic simulations.
In: Handbook of Numerical Analysis, Vol. XIV: Computational Methods
for the Ocean and the Atmosphere, P. G. Ciarlet, editor, R. Temam
& J. Tribbia, guest eds., Elsevier Science, pp. 121-183,
doi:10.1016/S1570-8659(08)01202-0 ,
PDF preprint
Capet, X., J. C. McWilliams, M. Molemaker, and A. F. Shchepetkin, 2008:
Mesoscale to submesoscale transition in the California current system.
Part I: Flow structure, eddy flux, and observational tests. J.
Phys. Oceanogr., 38, pp. 29-43,
doi:10.1175/2007JPO3671.1
Capet, X., J. C. McWilliams, M. Molemaker, and A. F. Shchepetkin, 2008:
Mesoscale to submesoscale transition in the California current system.
Part II: Frontal processes. J. Phys. Oceanogr., 38, pp. 44-64,
doi:10.1175/2007JPO3672.1
Capet, X., J. C. McWilliams, M. Molemaker, and A. F. Shchepetkin, 2008:
Mesoscale to submesoscale transition in the California current system.
Part III: Energy balance and flux. J. Phys. Oceanogr., 38,
pp. 2256-2269,
doi:10.1175/2008JPO3810.1
Kanarska, Y., A. Shchepetkin, and J. C. McWilliams, 2007: Algorithm for
non-hydrostatic dynamics in ROMS. Ocean Modeling, 18, pp.
143-174,
doi:10.1016/j.ocemod.2007.04.001
Dong, C., J. C. McWilliams and A. F. Shchepetkin 2006: Island wakes
in deep water, J. Phys. Oceanogr., 37, pp. 962-981,
doi:10.1175/JPO3047.1
Shchepetkin, A. F. and J. C. McWilliams: The regional oceanic modeling
system (ROMS): A split-explicit, free-surface, topography-following-coordinate
oceanic model. 2003 manuscript JCOMP-D-03-00102
from The Journal of Computational Physics;
eventually published in 2005, Ocean Modeling, 9/4,
pp. 347-404,
doi:10.1016/j.ocemod.2004.08.002 ,
PDF preprint
Shchepetkin, A. F., and J. C. McWilliams, 2003: A method for computing
horizontal pressure-gradient force in an oceanic model with a nonaligned
vertical coordinate, J. Geophys. Res., 108(C3), p. 3090,
doi:10.1029/2001JC001047 ,
PDF preprint
Marchesiello, P., J. C. McWilliams, and A. Shchepetkin, 2003: Equilibrium
structure and dynamics of the California Current System. J. Phys.
Oceanogr., 33 (4), pp. 753-783,
doi:10.1175/1520-0485(2003)33<753:ESADOT>2.0.CO;2
Ezer, T., H. Arango, and A. F. Shchepetkin, 2002: Developments in
terrain-following ocean models: intercomparison of numerical aspects.
Ocean Modeling 4, pp. 249-267.
doi:10.1016/S1463-5003(02)00003-3
Marchesiello, P., J. C. McWilliams, and A. F. Shchepetkin, 2001:
Open boundary condition for long-term integration of regional oceanic
models. Ocean Modeling 3, pp. 1-20.
doi:10.1016/S1463-5003(00)00013-5
Hardenberg, von J., J. C. McWilliams, A. Provenzale, A. Shchepetkin, and
J. B. Weiss, 2000: Vortex merging in quasi-geostrophic flows.
J. Fluid Mech., 412, pp. 331-353.
doi:10.1017/S0022112000008442
Haidvogel, D. B., H. Arango, K. Hedstrom, A. Beckmann, P. Rizzoli, and
A. F. Shchepetkin, 2000: Model evaluation experiments in the North
Atlantic Basin: Simulations in non-linear terrain-following
coordinates. Dyn. Atmos. Oceans, 32, pp. 239-281,
doi:10.1016/S0377-0265(00)00049-X
Shchepetkin, A. F. and J. C. McWilliams, 1998: Quasi-monotone advection
schemes based on explicit locally adaptive dissipation, Monthly
Weather Rev., 126, pp. 1541-1580,
doi:10.1175/1520-0493(1998)126<1541:QMASBO>2.0.CO;2 ,
PDF preprint
Yavneh, I., A. F. Shchepetkin, J. C. McWilliams, and L. P. Graves,
1997: Multigrid solution of rotating, stably stratified flows: The balance
equations and their turbulent dynamics; J. Comp. Phys., 136,
pp. 245-262,
doi:10.1006/jcph.1997.5775
Shchepetkin, A. F. and J. J. O'Brien, 1996: A physically consistent
formulation of lateral friction in shallow water equation ocean models,
Monthly Weather Review, 124, pp. 1285-1300,
doi:10.1175/1520-0493(1996)124<1285:APCFOL>2.0.CO;2
Meacham, S. P., K. K. Pankratov, A. F. Shchepetkin, and V. V. Zhmur,
1994: The interaction of arbitrarily oriented ellipsoidal vortices in
a continuously stratified fluid with background shear and strain flows,
Dyn. Atmos. Oceans, 21, pp. 167-212,
doi:10.1016/0377-0265(94)90008-6
Zhmur, V. V. and A. F. Shchepetkin, 1992: Interaction between two
quasigeostrophic vortices: tendency to come together and merge.
Atmos. Oceanic Phys., Russ. Acad. of Sci., 28, 407-416.
Zhmur, V. V. and A. F. Shchepetkin, 1991: Evolution of an ellipsoidal
vortex in a stratified ocean in the f-plane approximation.
Atmos. Oceanic Phys., Russ. Acad. of Sci., 27, pp. 331-346.
In preparation/under review
Shchepetkin, A. F. and J. C. McWilliams, 2003:
A family of finite-volume methods for computing pressure
gradient force in an ocean model with topography-following
vertical coordinate.
Presentations and Talks:
Shchepetkin, A. F.: An Adaptive, Courant-number-dependent implicit scheme
for vertical advection in oceanic models. 2014 Ocean Science Meeting,
Honolulu, HI, February 24 - 28, 2014.
PDF
Shchepetkin, A. F.: Numerically Accurate treatment of bottom drag in ocean
models with mode and time splitting. 2012 Ocean Science Meeting,
Salt Lake Sity, UT, February 20-24, 2012.
PDF
Shchepetkin, A. F.: Numerically Delicate Aspects of Splitting Decisions
Made in Ocean Modeling Codes. Irreducible Uncertainty BRC Meeting,
New York, NY, December 1 - 2, 2011,
PDF
Shchepetkin, A. F.: Rethinking mode splitting, splitting in general,
Boussinesq, non-Boussinesq, seawater EOS, and how it all comes together.
ROMS/TOMS User Workshop, Honolulu, HI, April 5 - 8, 2010
PDF
Shchepetkin, A. F., J. Molemaker, F. Colas, E. Mason, Y. Uchiyama, J. Kurian,
and J. C. McWilliams: Recent Developments of ROMS at UCLA. Physical
Oceanography Review Symposium Chicago, IL, June 7-13, 2009
PDF
Shchepetkin, A. F.: 10 years of ROMS project: An overview with emphasis
of what is overlooked, overdue, or missing. ROMS/TOMS Workshop and
Community Sediment Transport Modeling (CSTM) Meeting, Los Angeles, CA,
October 1-5, 2007.
PDF
Shchepetkin, A. F.: If-less KPP. ROMS/TOMS Workshop: Adjoint Modeling
and Applications, La Jolla, CA, October 24-28, 2005.
PDF
Shchepetkin, A. F.: Overview of evolution of computational kernel of ROMS:
How different things add up to make an ocean model. invited lecture at
ROMS/TOMS European Workshop, CNR-ISMAR, Venice, Italy, 17-21 October,
2004.
PDF
Shchepetkin, A. F.: Poor Man's Computing Revisited ROMS/TOMS European
Workshop, CNR-ISMAR, Venice, Italy, 17-21 October, 2004.
PDF
Shchepetkin, A. F.: KPP Implementation in ROMS. POM/ROMS Users
Workshop, PMEL NOAA, Seattle, WA, August 4-6, 2003
Shchepetkin, A. F.: The New Computational Kernel of ROMS. An invited
lecture in 2001 Terrain-Following Ocean Models Workshop, Boulder, CO,
August, 20-22, 2001
Shchepetkin, A. F.: The Regional Ocean Modeling System (ROMS): Time stepping
and time splitting algorithms. A presentation in Layered Ocean Model
Workshop. Miami, FL, 26-28 February 2001.
Shchepetkin, A. F.: High-order accuracy, monotonic continuous field
reconstruction on nonuniform grids. A presentation in Layered Ocean
Model Workshop. Miami, FL, 26-28 February 2001.
Shchepetkin, A. F., 1995, Interaction of turbulent barotropic shallow-water
flow with Topography,
1995 Proceedings of Hawaiian Winter Aha Huliko'a Workshop,
P. Müller and D. Henderson, editors, Honolulu, HI, pp. 225-237.
PDF
Shchepetkin, A. F. and S. P. Meacham, 1994, Interaction of intense mesoscale
vortices in a continuously stratified ocean. Annales Geophysicae,
Part II, Oceans, Atmosphere, Hydrology and Nonlinear Geophysics; Suppl.
to vol. 12, p. C511, EGS Symp. Grenoble.
Shchepetkin, A.F., 1993, On instabilities of vortices in the background
shear and strain flow. Preprints of the Ninth Conference of Atmospheric
and Oceanic Waves and Stability, p. 78-81. San Antonio, TX, 10-14 May, 1993.
Zhmur V. V. and A. F. Shchepetkin, 1991, Nonlinear evolution of
quasigeostrophic vortices in horizontal and vertical shear flow
in a stratified ocean. Abstracts of IAMAP Symposium,
M6, p. 103.
Zhmur V. V. and A. F. Shchepetkin, 1991, Interaction of baroclinic
quasigeostrophic vortices in a continuously stratified ocean.
Abstracts of IAMAP Symposium, Vienna, M6, p. 104.














